What makes non-Euclidean geometry so different?

You’re here — which means you’ve probably read that weird line in your math book: “Euclidean geometry is not the only geometry.” And now you’re like, “Wait… what other kind of geometry are we talking about?! And why does it sound like we just entered a parallel universe?”

Let’s ditch the textbook fog and break it all down like we’re sitting on a bench, chillin’, and talking wild math truths.

What Makes Non-Euclidean Geometry So Different?

Okay, first — let’s talk about what “Euclidean” even means. That word comes from Euclid, a Greek guy from 2,000+ years ago who basically wrote the rulebook for what we now call “normal” geometry — the kind you learned with triangles, parallel lines, and right angles.

But here’s the kicker: all of that only works in flat space. Like, on paper. 📄

Once space starts curving — like on a globe or in wild cosmic regions — those rules? Yeah, they start falling apart. And that’s where non-Euclidean geometry steps in like, “Don’t worry, I got this.” 😎

—

🧱 1. The Big Deal: The Parallel Postulate (And Why It Breaks)

At the heart of Euclidean geometry is a super famous rule called the parallel postulate. It basically says:

“If you draw a straight line, and pick a point not on it, there’s exactly one other line through that point that never touches the first one — aka, it’s parallel.”

Sounds normal, right?

But… what if space isn’t flat?

• On a sphere (like Earth), straight lines (which are really big circles) curve and eventually meet.
• In other kinds of warped spaces, you might get:
  • Zero lines that stay parallel 🔄
  • Or an infinite number of lines that never intersect 🌀

This is the moment where geometry takes the red pill and exits the Matrix. Welcome to non-Euclidean.

—

🌍 2. Two Main Types of Non-Euclidean Geometry

There are a few versions, but here are the two big ones:

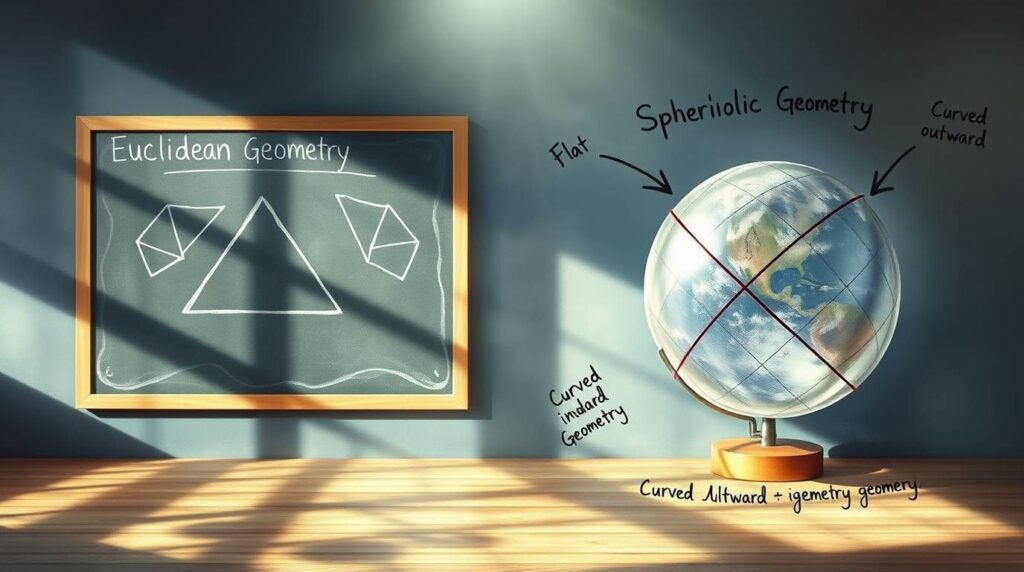
a) Spherical Geometry — Think Globes and Planets 🌐

• Lines are actually great circles (like the equator or the lines of longitude).
• The sum of angles in a triangle is more than 180°.
• Parallel lines? Nope. Everything eventually curves back and meets.
• Imagine walking straight on Earth — you’ll eventually loop around and bump into your own path.

Used in: GPS, astronomy, Earth mapping.

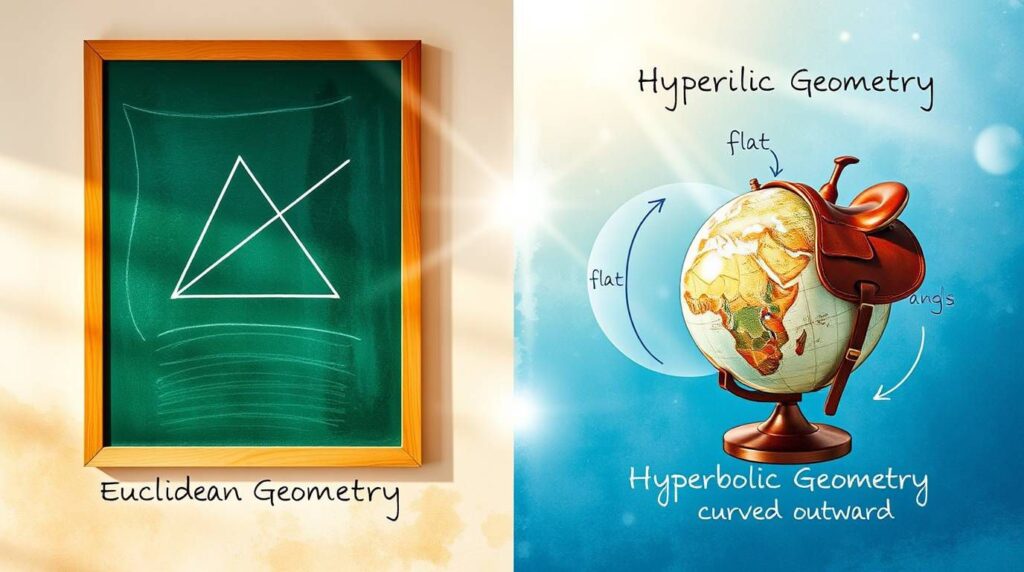
b) Hyperbolic Geometry — The Wild One 🔮

• Space curves outward like a Pringle chip or a saddle.
• The sum of triangle angles is less than 180°.
• Through a single point, there are infinite lines that don’t meet the original line — like a web of non-parallel possibilities.

Used in: Einstein’s theory of general relativity, black hole physics, and some seriously trippy art (shoutout to M.C. Escher).

—

🔍 3. So… Why Does It Even Matter?

Non-Euclidean geometry isn’t just math nerd fuel — it literally helps explain the real world.

• 🪐 Einstein used it to describe how gravity curves space and time.
• 🌎 It’s used in GPS tech to map Earth’s curved surface accurately.
• 🧠 It forces us to question our assumptions — like the idea that “space is flat,” which it totally isn’t in a lot of cases.

Basically, Euclidean geometry is like: “Here’s how shapes work on paper.”
Non-Euclidean is like: “Here’s how shapes work in the universe.” 🌌

—

🧠 TL;DR — Quick Summary:

• Euclidean geometry = normal shapes in flat space.
• Non-Euclidean geometry = wild shapes in curved space.
• Main difference? It’s all about how parallel lines behave.
• Two types:
  • Spherical = triangles with >180°, no parallels.
  • Hyperbolic = triangles with <180°, infinite parallels.
• It’s not just theoretical — it’s used in physics, navigation, and cosmology.

—

📌 Disclaimer:
This easy version is meant to help you understand the concept better. If your exam or teacher expects a textbook explanation and you write this one instead, we’re not responsible if it affects your marks. Use this for understanding, not copy-pasting.

—

🔗 Related Articles from EdgyThoughts.com:

Why Is Eigenvalue Decomposition So Important?
https://edgythoughts.com/why-is-eigenvalue-decomposition-so-important/

What If Reality Is a Simulation Running on Light? 2025
https://edgythoughts.com/what-if-reality-is-a-simulation-running-on-light-2025

🌐 External Resource:
Curious how mathematicians proved these ideas? Read the Wikipedia article:
https://en.wikipedia.org/wiki/Non-Euclidean_geometry